
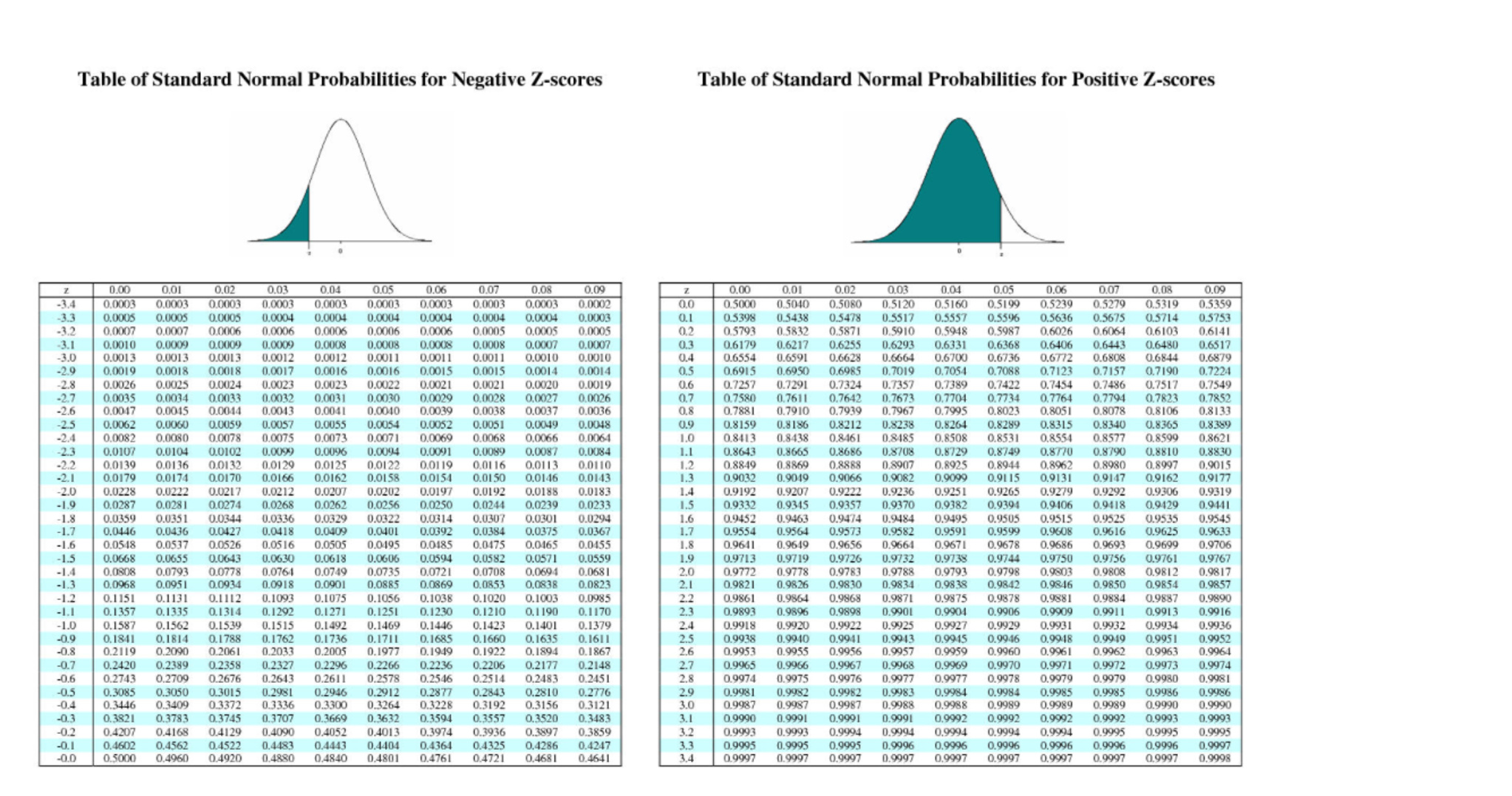
If you want to find the value between z=0 and a positive number, use the right-hand z-table (above) instead (Hint: if you’re asked to look at the “z-table”, in most cases you’ll want to be looking at the other z-table!)īeyer, W. In other words, the area of a left hand tail. This table shows the area to the left of Z. For an area in a left tail, look at this left-tail z-table instead. Use these values to find the area between z=0 and any positive value. This z-table (normal distribution table) shows the area to the right hand side of the curve. It tells us the area under the standard normal curve for any value between the mean (zero) and any z-score. But what about if we want to know the area between z = -0.78 and z = 0.78? Or z = -1.2 and z=0.44? That’s where the z-table comes in.
The above graph can tell us the area under the curve for one (z = -1 to 1), two (z = -2 to 2) and three (z = -3 to 3) standard deviations from the center. Obviously a graph can only give us so much information. On this graph, it’s represented by two z-scores from the z table: the area between z = -1 and z = 1. For example, 68.27 percent of results will fall within one standard deviation of the mean. This graph shows the standardized normal graph with the percentage of results (data) that will fall between standard deviations on that graph. When the curve is standardized, we can use a Z Table to find percentages under the curve. Those wide ranges make it difficult to analyze data, so we “standardize” the normal curve, setting it to have a mean of zero and a standard deviation of one. For example, heights of people might range from eighteen inches to eight feet and weights can range from one pound (for a preemie) to five hundred pounds or more.
What is a Z Table: Standard Normal ProbabilityĮvery set of data has a different set of values.


 0 kommentar(er)
0 kommentar(er)
